Using Maxima in Calculus

1 Plotting examples

--> plot2d ( sin ( x ) , [ x , 0 , 1 ] ) ;
--> example ( plot3d ) ;
--> plot3d ( x ^ 2 + y ^ 2 , [ x , − 5 , 5 ] , [ y , − 5 , 5 ] , [ gnuplot_pm3d , true ] ) $
--> example ( wxplot3d ) ;

Call the wx-version of a routine to show pictures inline:

(%i1) wxplot3d ( [ 5 · cos ( x ) · ( cos ( x / 2 ) · cos ( y ) + sin ( x / 2 ) · sin ( 2 · y ) + 3 . 0 ) − 10 . 0 ,
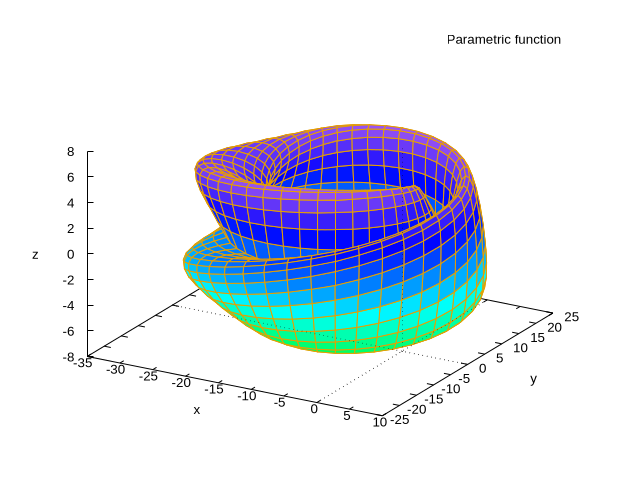
      − 5 · sin ( x ) · ( cos ( x / 2 ) · cos ( y ) + sin ( x / 2 ) · sin ( 2 · y ) + 3 . 0 ) ,
       5 · ( − sin ( x / 2 ) · cos ( y ) + cos ( x / 2 ) · sin ( 2 · y ) ) ] ,
      [ x , − %pi , %pi ] , [ y , − %pi , %pi ] , [ ' grid , 40 , 40 ] ) $

\[\tag{%t1} \]

(Graphics)
(%i3) wxplot2d ( [ atan ( x ) , %pi / 2 , − %pi / 2 ] , [ x , − 10 , 10 ] , [ color , blue , magenta , brown ] ) $

\[\tag{%t3} \]

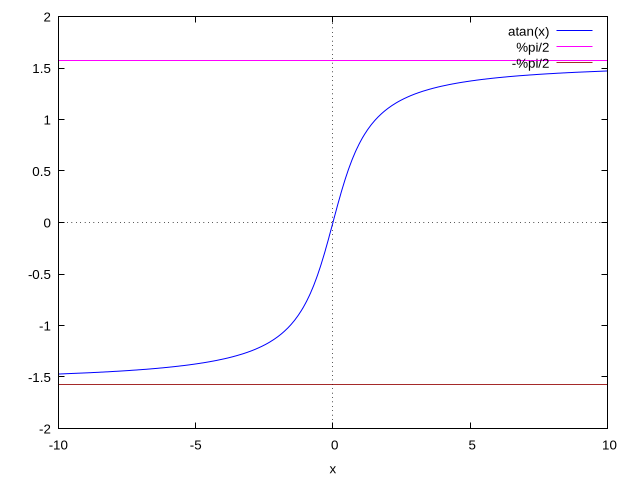
(Graphics)

This will display the result in a popup window:

--> plot2d ( x ^ 2 · exp ( − x ^ 3 / 1000 ) , [ x , 0 , 20 ] ) $

2 Integrate

--> integrate ( 1 / ( x + x · sqrt ( x ) ) , x ) ;
--> fullratsimp ( % ) ;

(% refers to the output of the previous evaluation)

--> integrate ( ( 1 − tan ( x ) ^ 2 ) / sec ( x ) ^ 2 , x ) ;
--> trigsimp ( % ) ;
--> integrate ( x ^ 2 / sqrt ( 1 + x ^ 2 ) , x ) ;
--> integrate ( 1 / sqrt ( 16 − x ^ 2 ) ^ 3 , x ) ;
--> integrate ( ( log ( x ) + 5 ) / ( x · ( log ( x ) ^ 2 + 4 ) ) , x ) ;

3 Find roots of a polynomial

--> allroots ( x ^ 10 − 2 · x ^ 4 + 1 / 2 ) ;

4 Applying "at"

--> Values : [ a = 10 , c = 100 ] ;
   Pyth : a ^ 2 + b ^ 2 = c ^ 2 ;
   solve ( % , b ) ;
   result : % [ 2 ] ;
   at ( result , Values ) ;
   float ( % ) ;
-->   g1 : a · x + y = 0 ;
   g2 : b · y + x · x = 1 ;
   solve ( [ g1 , g2 ] , [ a , b ] ) ;
   % [ 1 ] ;
   result_b : b = at ( b , % ) ;
-->    ohm : U = R · I ;
   r_parallel : R = R_1 · R_2 / ( R_1 + R_2 ) ;
   result : at ( ohm , r_parallel ) ;
--> example ( at ) ;

5 Direction fields

--> plotdf ( x − y ^ 2 , [ xfun , "sqrt(x);−sqrt(x)" ] ,
        [ trajectory_at , − 1 , 3 ] , [ direction , forward ] ,
        [ y , − 5 , 5 ] , [ x , − 4 , 16 ] ) $
--> plotdf ( [ y , − ( k · x + c · y + b · x ^ 3 ) / m ] ,
            [ parameters , "k=−1,m=1.0,c=0,b=1" ] ,
            [ sliders , "k=−2:2,m=−1:1" ] , [ tstep , 0 . 1 ] ) ;
--> plotdf ( [ w , − g · sin ( a ) / l − b · w / m / l ] , [ a , w ] ,
       [ parameters , "g=9.8,l=0.5,m=0.3,b=0.05" ] ,
       [ trajectory_at , 1 . 05 , − 9 ] , [ tstep , 0 . 01 ] ,
       [ a , − 10 , 2 ] , [ w , − 14 , 14 ] , [ direction , forward ] ,
       [ nsteps , 300 ] , [ sliders , "m=0.1:1" ] , [ versus_t , 1 ] ) $
--> plotdf ( x ^ 2 · y , [ trajectory_at , . 1 , 1 ] ) $

5.1 Examples from class

--> plotdf ( x ^ 2 · y ,
        [ y , − 5 , 5 ] , [ x , − 5 , 5 ] ) $

Electric circuit example:

--> plotdf ( 15 − 3 · y , [ xfun , "5" ] ,
        [ y , − 1 , 10 ] , [ x , − 1 , 10 ] ) $

Orthogonal trajectories example:

--> plotdf ( − 2 · x / y , [ xfun , "sqrt(x);2·sqrt(x);sqrt(x);3·sqrt(x);−sqrt(x)" ] ,
        [ y , − 10 , 10 . 1 ] , [ x , − 10 , 10 ] ) $

Tank example:

--> plotdf ( ( 150 − y ) / 200 , [ xfun , "150" ] ,
        [ y , − 10 , 200 ] , [ x , − 10 , 2000 ] ) $

Logistic model:

--> plotdf ( 0 . 08 · P · ( 1 − P / 1e3 ) , [ t , P ] , [ P , 0 , 1400 ] , [ t , 0 , 80 ] , [ xfun , "1000" ] ) $

Logistic model vs natural growth:

--> plot2d ( [ 1000 / ( 1 + 9 · exp ( − 0 . 08 · t ) ) , 1000 , 100 · exp ( 0 . 08 · t ) ] , [ t , 0 , 80 ] , [ y , 0 , 1400 ] , [ color , blue , magenta , red ] , [ style , [ lines , 3 ] ] ) $

Logistic model with harvesting:

--> plotdf ( 0 . 08 · P · ( 1 − P / 1e3 ) − 35 , [ t , P ] , [ P , 0 , 1400 ] , [ t , 0 , 80 ] , [ xfun , "1000" ] ) $

Logistic model with minimal population:

--> plotdf ( 0 . 08 · P · ( 1 − P / 1e3 ) · ( 1 − 2e2 / P ) − 5 , [ t , P ] , [ P , 0 , 1400 ] , [ t , 0 , 80 ] , [ xfun , "1000; 200" ] ) $

6 Solving differential equations with ode2

--> y ^ 2 · ' diff ( y , x ) = x ^ 2 ;
--> ode2 ( % , y , x ) ;
--> solve ( % , y ) ;
--> ' diff ( y , x ) = x ^ 2 · y ;
--> ode2 ( % , y , x ) ;

Initial conditions:

--> ' diff ( y , x ) = y / x + 1 ;
ode2 ( % , y , x ) ;
--> ' diff ( y , x ) = 2 · x · y ^ ( 1 / 3 ) ;
ode2 ( % , y , x ) ;
--> ic1 ( % , x = 3 , y = 0 ) ;
--> ' diff ( y , x ) = − exp ( x + 3 · y ) ;
--> ode2 ( % , y , x ) ;
--> ic1 ( % , x = 8 , y = 1 ) ;
--> integrate ( 2 · %pi · ( x ^ 2 / 4 − log ( x ) / 2 ) · ( x / 2 + 1 / ( 2 · x ) ) , x ) ;
--> integrate ( 2 · %pi · ( x ^ 2 / 4 − log ( x ) / 2 ) · ( x / 2 + 1 / ( 2 · x ) ) , x , 1 , 2 ) ;

7 Polar plots

--> draw2d ( nticks = 800 , xrange = [ − 10 , 10 ] , yrange = [ − 10 , 10 ] ,
   polar ( theta / ( 2 · %pi ) , theta , 0 , ( 20 · %pi ) ) ) $
--> draw2d ( nticks = 80 , xrange = [ − 10 , 10 ] , yrange = [ − 10 , 10 ] ,
   polar ( 2 + 4 · cos ( 3 · theta ) , theta , 0 , ( 2 · %pi ) ) ) $
--> draw2d ( nticks = 80 , xrange = [ − 12 , 12 ] , yrange = [ − 12 , 12 ] ,
   [ polar ( 6 + 5 · sin ( theta ) , theta , 0 , ( 2 · %pi ) ) ,
   polar ( 6 + 5 · cos ( theta ) , theta , 0 , ( 2 · %pi ) ) ] ) $
--> draw2d ( nticks = 80 , xrange = [ − 10 , 10 ] , yrange = [ − 10 , 10 ] ,
   polar ( 2 · cos ( theta / 2 ) , theta , 0 , ( 4 · %pi ) ) ) $
--> draw2d ( nticks = 200 , xrange = [ − 12 , 12 ] , yrange = [ − 12 , 12 ] ,
   [ polar ( sqrt ( cos ( 4 · theta ) ) , theta , 0 , 2 · %pi ) ,
   polar ( − sqrt ( cos ( 4 · theta ) ) , theta , 0 , 2 · %pi ) ] ) $

Cardioid:

--> draw2d ( nticks = 80 , xrange = [ − 10 , 10 ] , yrange = [ − 10 , 10 ] ,
   polar ( 1 +   sin ( theta ) , theta , 0 , 2 · %pi ) ) $

7.1 Conic sections

--> draw2d ( nticks = 80 , xrange = [ − 10 , 10 ] , yrange = [ − 10 , 10 ] ,
   polar ( 2 / ( 3 + 4 · cos ( theta ) ) , theta , 0 , 2 · %pi ) ) $

8 Implicit plots

-->    draw2d ( explicit ( x ^ 2 + x , x , − 4 , 3 ) , ip_grid = [ 400 , 400 ] , color = black ,
    implicit ( x ^ 2 + y ^ 2 + 6 · x − 4 · y − 7 , x , − 10 , 5 , y , − 10 , 10 ) ) $
--> draw2d ( ip_grid = [ 100 , 100 ] , implicit ( ( x − 1 ) ^ 2 + y ^ 2 = 3 , x , − 6 , 6 , y , − 6 , 6 ) ) $
--> load ( "implicit_plot" ) $
ip_grid : [ 100 , 100 ] $
--> implicit_plot ( [ 9 · y ^ 2 − 4 · x ^ 2 − 36 · y − 8 · x = 4 ,
       y − 2 = 2 · ( x + 1 ) / 3 ,
       y − 2 = − 2 · ( x + 1 ) / 3
   ] , [ x , − 10 , 10 ] , [ y , − 10 , 10 ] ) $
--> r : 4 · cos ( 3 · theta ) ;
--> integrate ( sqrt ( r ^ 2 + diff ( r , theta ) ^ 2 ) , theta , 0 , %pi / 6 ) ;
--> plot2d ( [ cos ( x ) ^ 2 − 1 / 2 , %pi ^ 2 / 32 − x ^ 2 / 2 ] , [ x , − %pi , %pi ] ) $

9 Series

--> sum ( 3 ^ ( 2 − 2 · k ) · 7 ^ k , k , 1 , inf ) ;
--> % , simpsum ;
--> % , numer ;

Created with wxMaxima.