mpLBFGS

A multiple precision L-BFGS implementation, allowing to find minimizers of unconstrained and simple constrained problems to (almost) any number of digits. It uses the template matrix classes from Eigen with the mpreal class in place of the usual scalars. Pictured: a 44-point spherical code in \(\mathbb R^6\), conjectured to have the largest pairwise separation, in a random orientation. It is also conjectured to be the support of a measure optimizing the continuous p-frame energy functional. This and other configurations were identified numerically as minimizers by obtaining high-precision representations of their pairwise scalar products.

BRieszk

/ˈbrisk/ is a selection of routines helpful in dealing with discrete measures converging to a continunous density. They will compute near-minimizers of varying quality for the Riesz energy-styled functionals. Several elementary underlying sets are built-in; general (well-behaved) implicit surfaces are supported. Proceed with care.

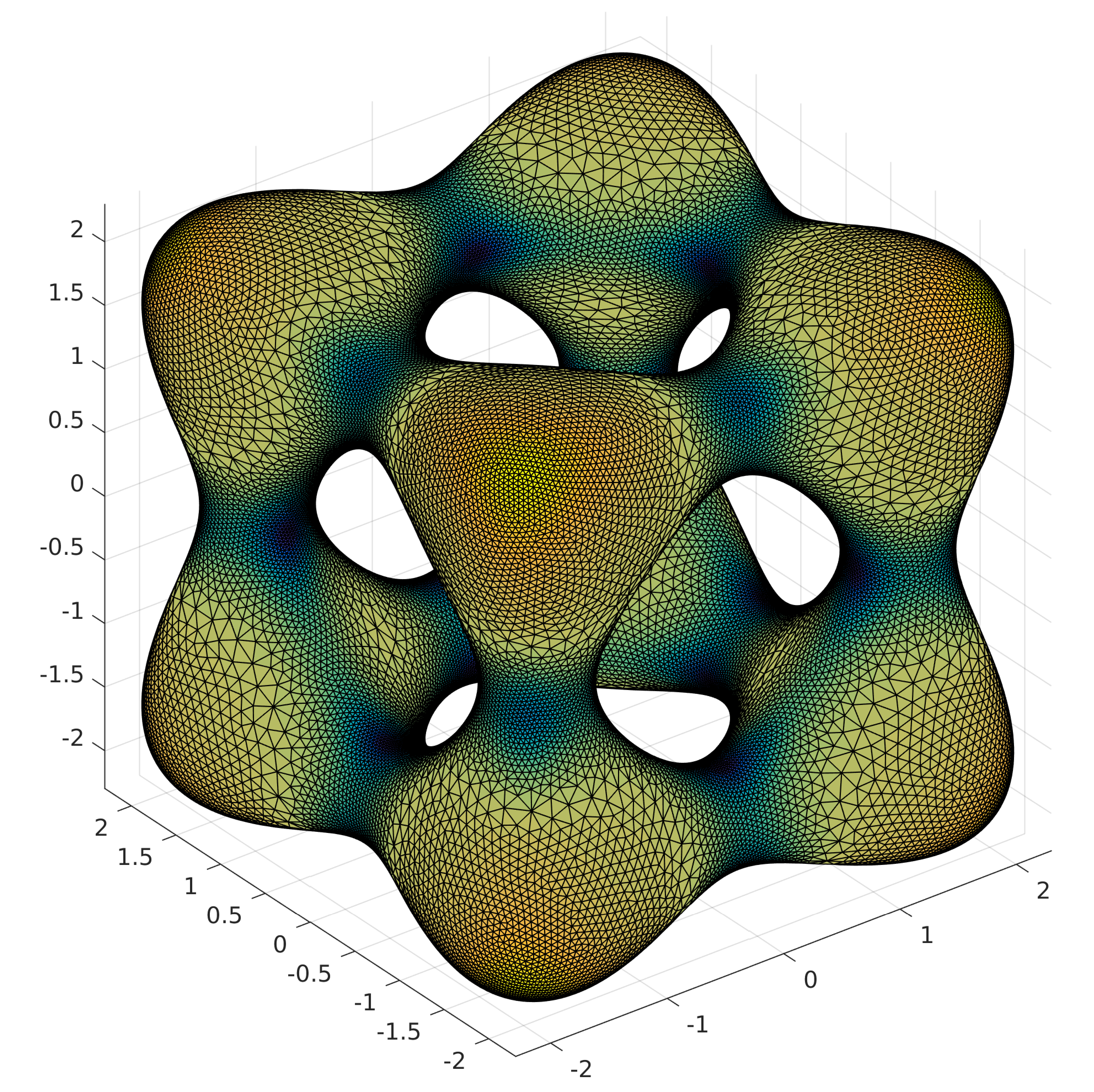
Below, for example, are 40,000 points on the tangle

distributed according to the absolute value of its Gaussian curvature.

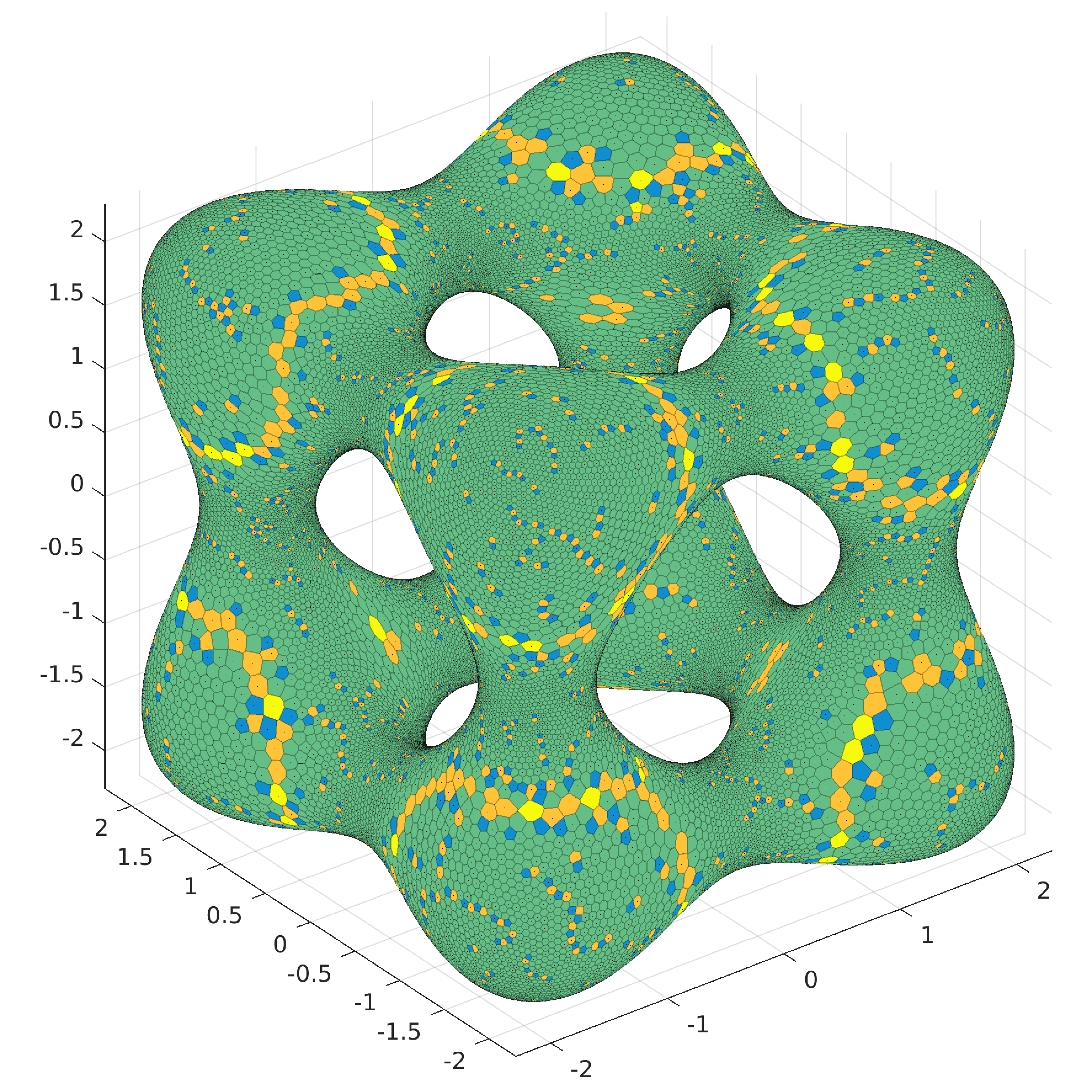
Left: (approximate) Delaunay triangulation with faces color-coded by the value (not the absolute value) of curvature, blue-orange/low-high; right: (approximate) Voronoi diagram with faces colored by the number of edges, blue-yellow/few-many (hexagons are the majority). Here the approximation is understood in the sense that both the Delaunay and Voronoi are computed locally in the tangent plane, then transplanted back to the surface. Notice also that the goal is never to reach an exact local minimizer of the respective energy, rather to emulate certain features of such minimizers. Accordingly, no Hessians are computed and no careful line searches performed. In fact, it is remarkable that these points aren’t terrible on the energy scale.

The Github repo for BRieszk is here. The proof that the approach of truncating interactions to a fixed number of nearest neighbors results in minimizers which have both the optimal local properties and the correct distribution is contained in the joined paper with D. P. Hardin and E. B. Saff, Asymptotic properties of short-range interaction functionals, arXiv:2010.11937.

3dRBFnodes

Along the same lines, one can produce reasonable nodes for RBF-functions and use the latter for, say, geomodelling. A reasonably scalable implementation can be found below; it handles up to 3M nodes in 3d on an i5 CPU laptop. There is nonempty code overlap with BRieszk. A detailed discussion is contained in the paper.

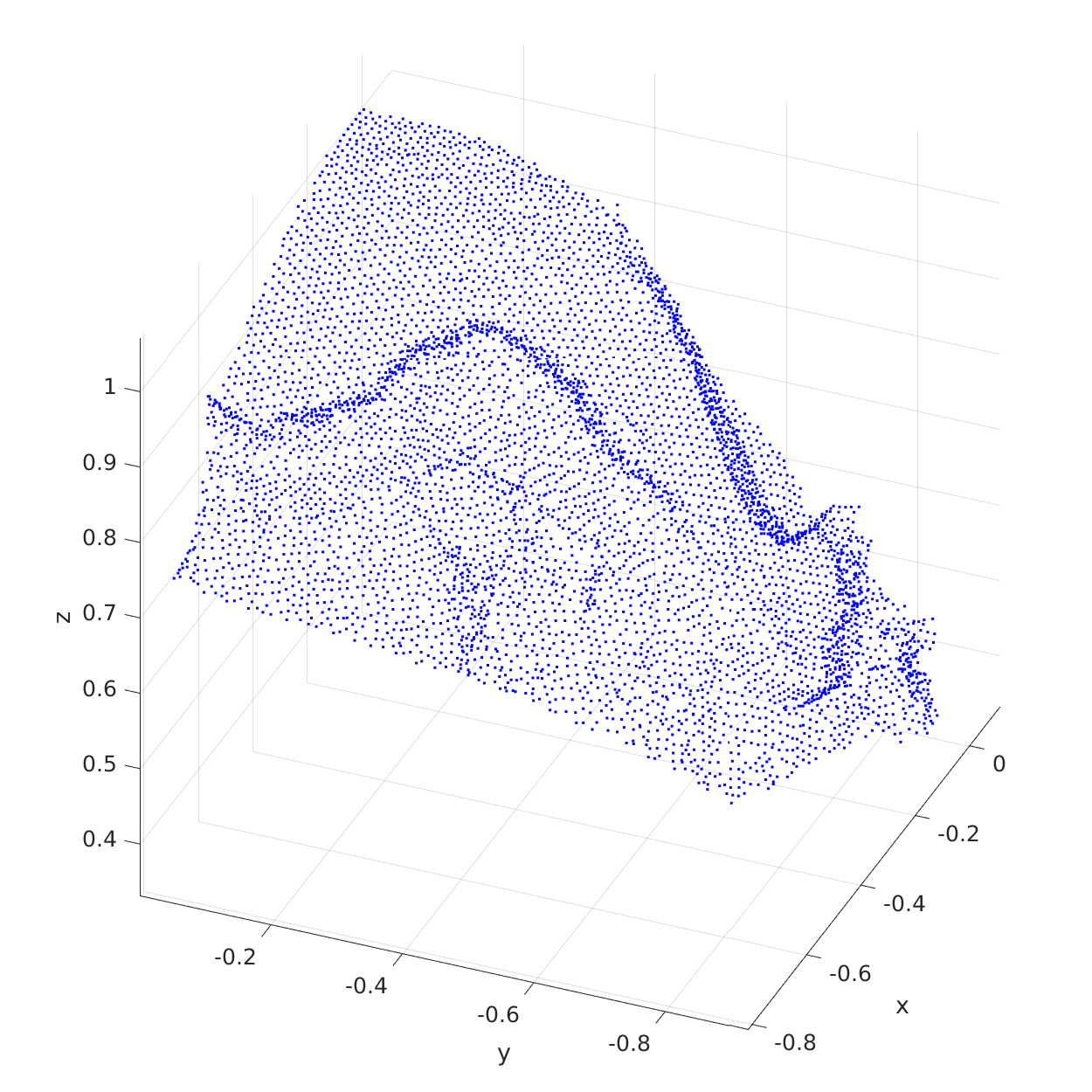
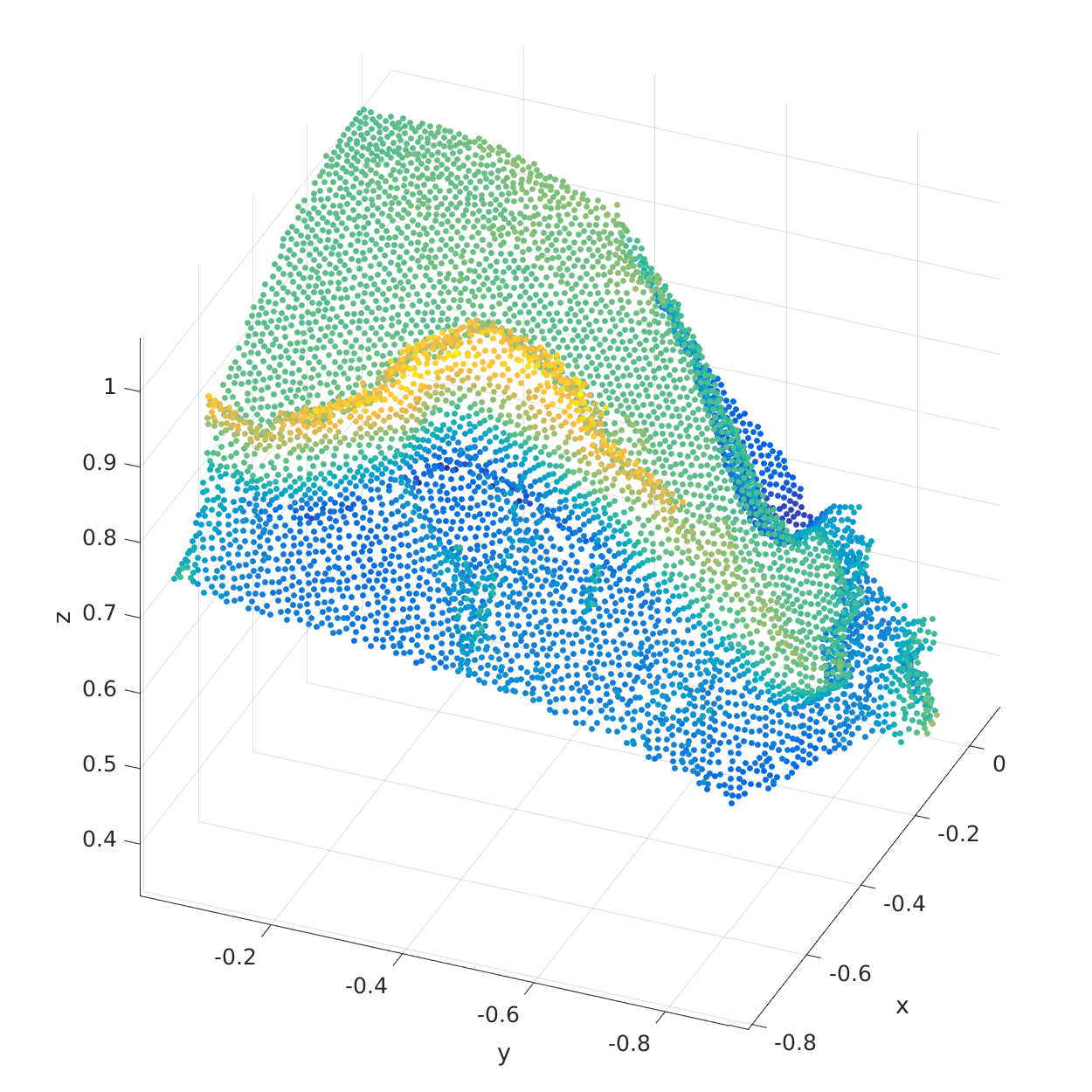
The Github repo for 3dRBFnodes is here. Below are two pictures showing Andes, the one on the right is color-coded by elevation.